Gelijk
Misvatting: De meeste energie wordt verbruikt in de lamp, daarom zal daar ook de grootste stroomsterkte lopen. Maar het is een serieschakeling, dus de stroomsterkte is op elk punt gelijk.

A In een serieschakeling is de stroomsterkte door elke component gelijik
B In een serieschakeling is de stroomsterkte door elke component gelijik
C Correct
D In een serieschakeling is de stroomsterkte door elke component gelijik

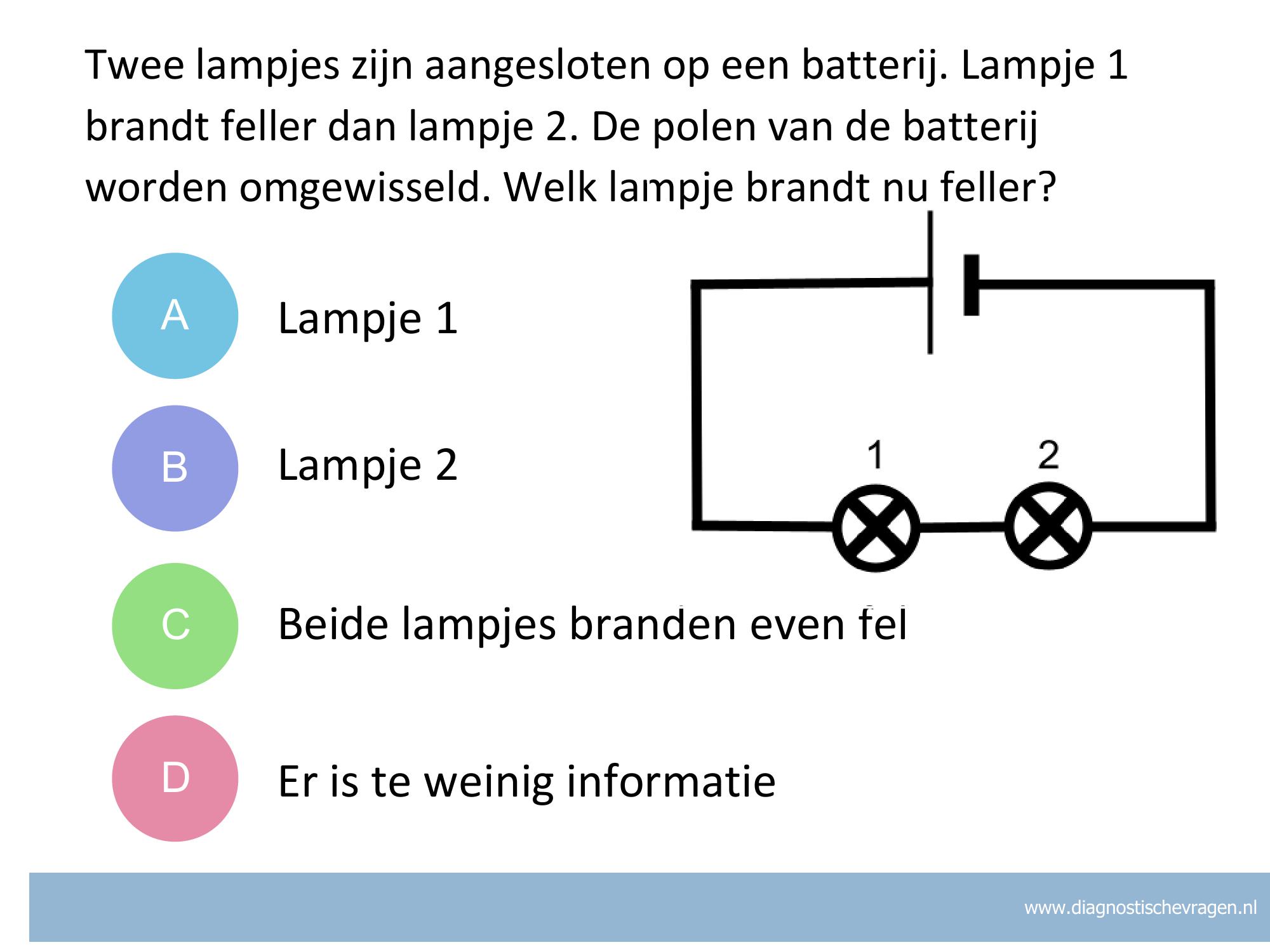
Misvatting:

A Lampje 1 heeft een grotere weerstand en brandt dus feller. Bij het wisselen van de polen van de batterij verandert er niets aan de weerstand van de lampjes. Lampje 1 brandt dus nog steeds feller.

B De spanning wordt verdeeld over de lampjes op basis van de weerstand van de lampjes. De spanning die een lampje krijgt heeft niet te maken met de volgorde van de lampjes.

C De lampjes zijn verschillend. Door het draaien van de batterij verandert er niets aan de weerstand van de lampjes.

D De spanning en de stroomsterkte zijn niet gegeven, toch kun je met redeneren deze vraag beantwoorden.

Misvatting:

A Je denkt misschien: Weinig weerstand betekent veel stroom. Maar bedenk je dat in een serieschakeling de stroom door elke component gelijk is. De spanning wordt verdeeld.

B Het lampje van 4 Ω brandt het felst. In een serieschakeling is de stroomsterkte door elke component gelijk. De lampjes krijgen dus evenveel stroom. Maar de spanning wordt verdeeld in dezelfde verhouding als de weerstanden. De spanning over het lampje van 4 Ω is dus 2x zo groot. Het vermogen P = U · I van die lamp is dus het grootst.

C De lampjes krijgen wel evenveel stroom (want het is een serieschakeling). Maar de spanning is niet even groot.

D De spanning en de stroomsterkte zijn niet gegeven, toch kun je met redeneren deze vraag beantwoorden.

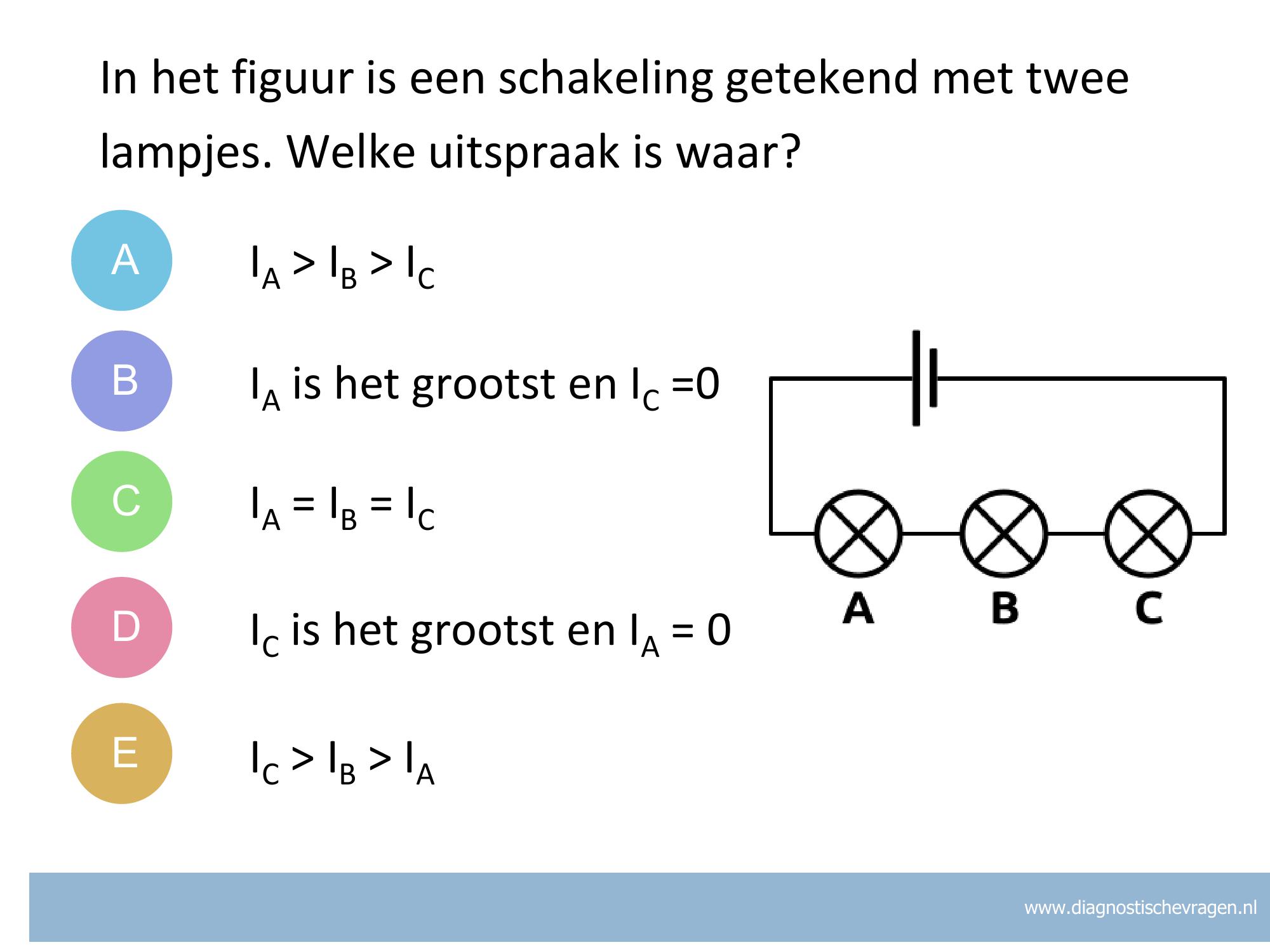
Misvatting:

A Je denkt waarschijnlijk dat lampje A meer stroom krijgt omdat die het dichste bij de batterij zit en de stroom van + naar – gaat, maar stroom wordt niet verbruikt. Alles staat in serie en dus is er maar 1 route voor de stroom.


B Je denkt waarschijnlijk dat lampje A meer stroom krijgt omdat die het dichste bij de batterij zit en de stroom van + naar – gaat, maar stroom wordt niet verbruikt. Alles staat in serie en dus is er maar 1 route voor de stroom.


C Correct. Alles staat in serie dus de stroom heeft maar 1 route om van de bron terug naar de bron te gaan.


D Je denkt waarschijnlijk dat lampje C meer stroom krijgt omdat die het dichste bij de batterij zit en de elektronen van – naar + stromen, maar stroom wordt niet verbruikt. Alles staat in serie en dus is er maar 1 route voor de stroom. De stroom gaat terug naar de bron.


E Je denkt waarschijnlijk dat lampje C meer stroom krijgt omdat die het dichste bij de batterij zit en de elektronen van – naar plus stromen, maar stroom wordt niet verbruikt. Alles staat in serie en dus is er maar 1 route voor de stroom.

Misvatting:

A Je denkt misschien: Meer lampjes hebben meer stroom nodig. Maar de spanning staat vast. De weerstand wordt groter, dus de stroomsterkte neemt af.

B Correct. Je hebt een vaste spanning en met meer lampjes neemt de weerstand in de schakeling toe

C Je denkt misschien: de stroomsterkte in een serieschakeling is constant. Maar de stroomsterkte in een serieschakeling kan wel veranderen. Alleen is op elk moment de stroomsterkte door elke component. Bijvoorbeeld: Mijn huis is evenveel waard als dat van mijn buurman, maar beide prijzen kunnen wel tegelijkertijd stijgen of dalen.

D Je denkt misschien dat je moet weten hoe groot de stroomsterkte is, maar dat maakt voor deze vraag niet uit

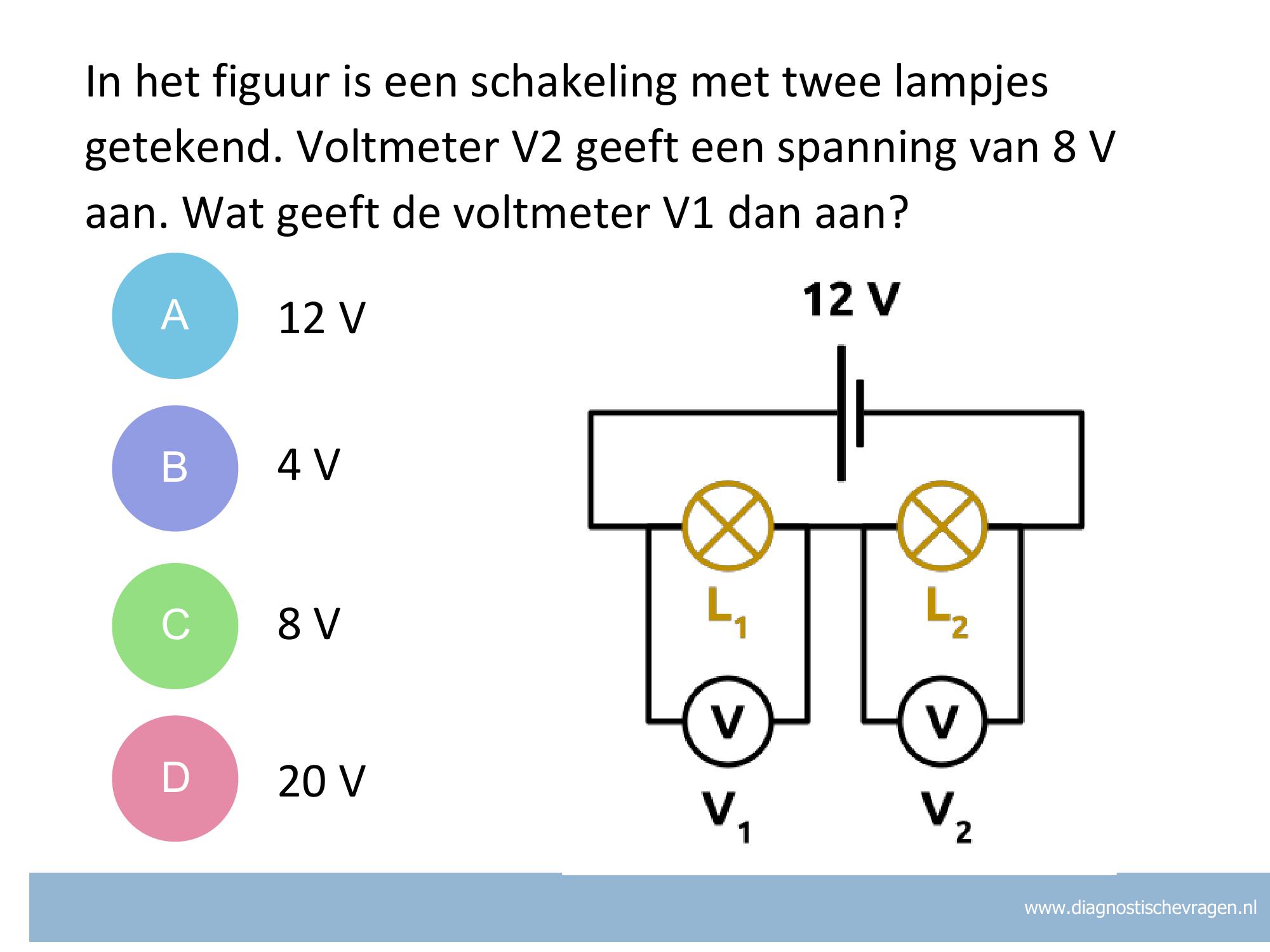
Misvatting:

A Omdat lampje 1 aan de plus-kant van de batterij zit, denk je misschien dat dat lampje de volledige spanning krijgt. Maar de spanning over een component is het verschil in energie van de elektronen vóór en ná die component. De volgorde van de lampjes maakt niet uit.

B De spanning in een serieschakeling wordt verdeeld over de componenten: Utot = U1 + U2. Invullen geeft 12 = U1 + 8 en dat geeft U1 = 4 V

C In een serieschakeling wordt de spanning verdeeld, maar niet altijd eerlijk! Hoe het precies verdeeld wordt, hangt af van de weerstand van de componenten. Hier is gegeven dat het ene lampje 8 (V) krijgt, en omdat er in totaal 12 V beschikbaar is, is er nog 4 V over voor het tweede lampje.

DJe gebruikt de formule al goed, maar je maakt een vergissing bij het ‘naar de andere kant halen’ van 8 V.

Misvatting:

A De regelbare weerstand wordt 3x zo groot, dus je denkt misschien dat de stroomsterkte 3x zo klein wordt. Maar de totale weerstand gaat van 200 Ω naar 400 Ω, dus 2x zo groot.

B Correct De totale weerstand van de schakeling neemt toe van 200 Ω naar 400 Ω. De weerstand wordt dus 2x zo groot. De spanning blijft gelijk, dus de stroomsterkte wordt 2x zo klein (U = I · R). De stroomsterkte is dus 30 mA

C Je denkt misschien: in een serieschakeling blijft de stroomsterkte constant. Maar de regel is: in een serieschakeling is de stroomsterkte door elke component gelijk. De totale stroomsterkte kan wel toe- of afnemen volgens U = I · R

D Je denkt misschien: de weerstand wordt 2x zo groot, dus de stroomsterkte wordt ook 2x zo groot. Maar in de formule U = I · R blijft de spanning U constant. De weerstand wordt 2x zo groot, dus dan moet de stroomsterkte wel 2x zo klein worden.

E Je denkt misschien: de weerstand wordt 3x zo groot, dus de stroomsterkte wordt ook 3x zo groot. Maar ten eerste wordt de totale weerstand slechts 2x zo groot (van 100 Ω naar 400 Ω. Ten tweede: in de formule U = I · R blijft de spanning U constant. De weerstand wordt 2x zo groot, dus dan moet de stroomsterkte wel 2x zo klein worden.

De totale weerstand van de schakeling is R = U/I = 5/1 = 5 Ω . Het is een serieschakeling, dus de totale weerstand is de som van de losse weerstanden. Dus R1 + R2 = 5 Ω. Dus R2 = 5 – 2 = 3 Ω
Misvatting:

A Je denkt misschien dat de verschillende weerstanden in een serieschakeling altijd gelijk moeten zijn. Dat is niet het geval

B Goed antwoord.

C Dit is de weerstand van de totale serieschakeling. Gevraagd is de weerstand van een component. Tip denk er aan welke

D Je hebt misschien gedaan R = U · I. Maar die vergelijking klopt niet, het moet zijn U = I · R

Misvatting:

A Correct. De weerstand in de parallelle schakeling neemt af en bij gelijke spanning wordt de stroomsterkte door de batterij dan groter

B Je denkt misschien dat de weerstand groter wordt met meer lampjes, maar het is een parallelschakeling en daar wordt de weerstand kleiner

C Je denkt misschien: de stroomsterkte in een serieschakeling is constant. Maar de stroomsterkte in een serieschakeling kan wel veranderen.

D Je denkt misschien dat je moet weten hoe groot de spanning van de batterij en de stroomsterktes zijn, maar dat is voor deze vraag niet relevant.

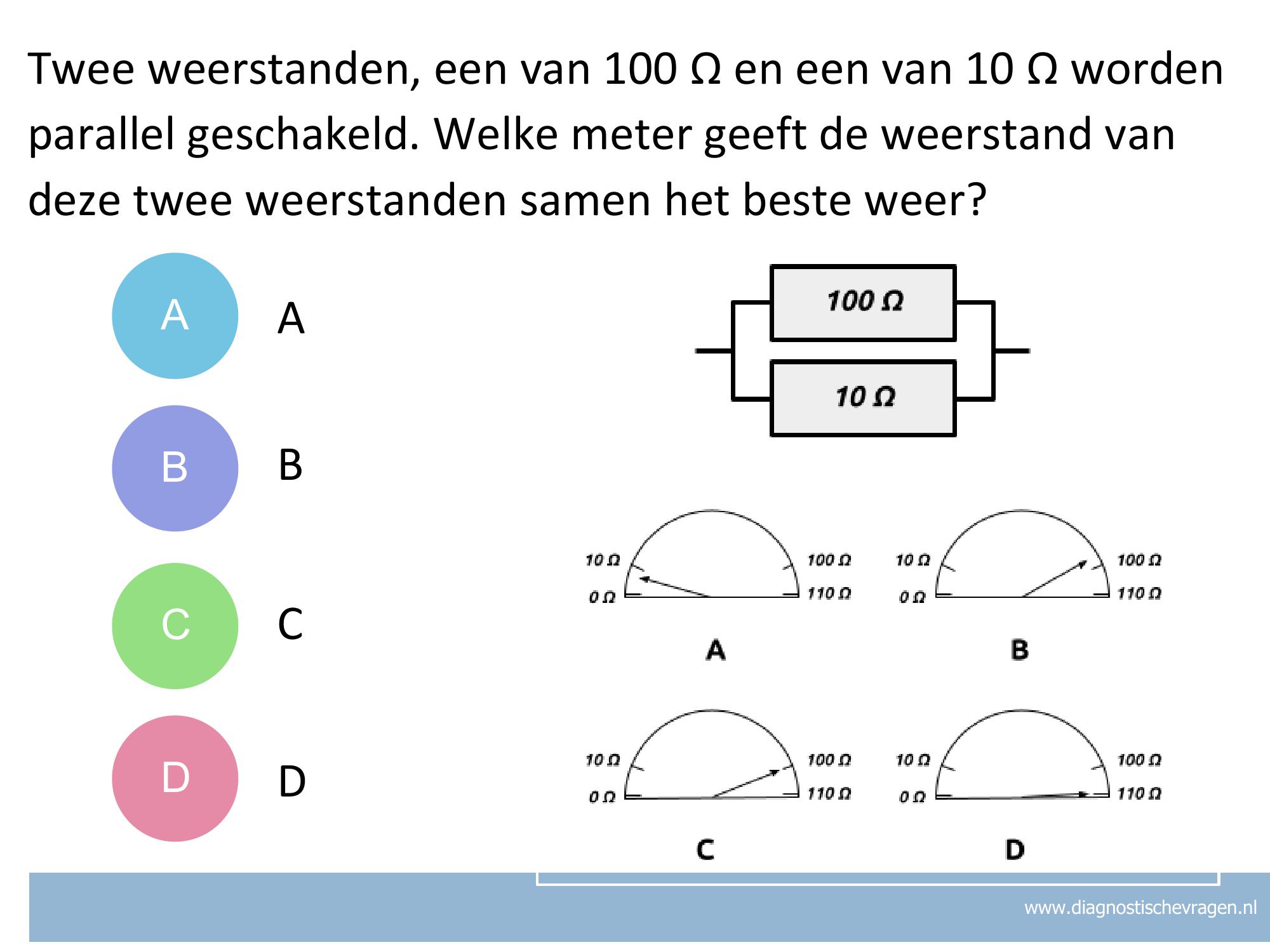
Misvatting:

A Correct. Elke extra weerstand die je parallel schakelt, opent een extra weg voor de stroom. De weerstand wordt dus altijd lager als er een extra tak bijkomt. De weerstand moet dus kleiner zijn dan 10 Ω, en dat is dus antwoord A.

B Je snapt al dat de totale weerstand kleiner moet zijn dan 100 Ω. Maar de totale weerstand moet ook kleiner dan 10 Ω zijn. Want er staat een andere weerstand parallel met die van 10 Ω.

C Je denkt dat de grootste weerstand telt. Maar in een parallelschakeling geldt voor weerstanden (1)/(Rtot) = (1)/(R1) + (1)/(R2). Daaruit volgt dat de totale weerstand kleiner is dan elk van de deelweerstanden.

D Je telt de weerstanden bij elkaar op. Dat mag alleen in een serieschakeling, maar dit is een parallelschakeling. Daarvoor geldt: (1)/(Rtot) = (1)/(R1) + (1)/(R2).

Misvatting:

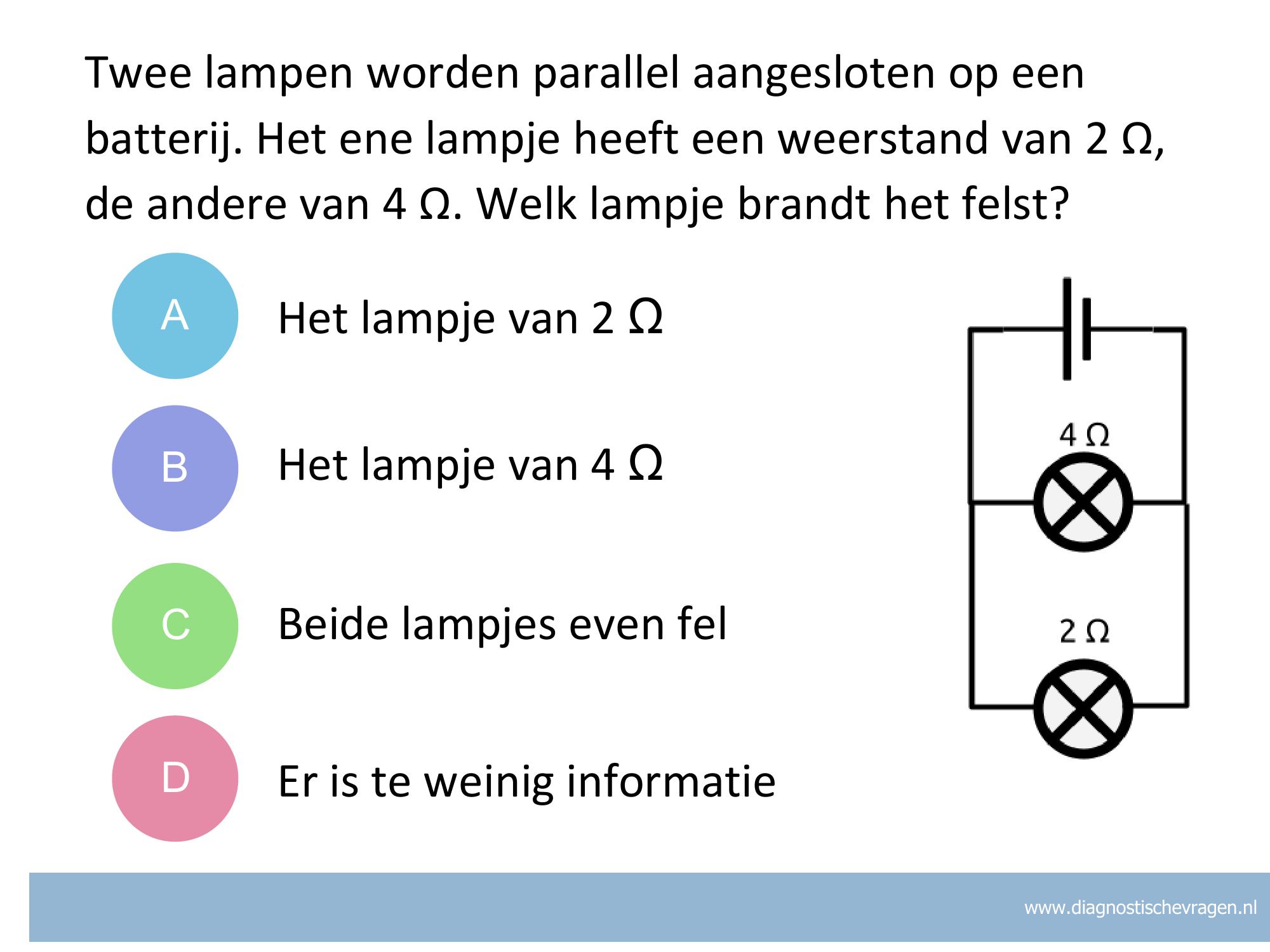
A Beide lampjes zijn als het ware rechtstreeks aangesloten op de batterij en branden dus op dezelfde spanning. Het lampje van 2 Ω heeft de kleinste weerstand. Er loopt door dit lampje de meeste stroom. Het vermogen P = U · I van die lamp is dus het grootst. Het lampje van 2 Ω brandt dus het felst.

B Je denkt waarschijnlijk dat het lampje met de grootste weerstand het felst brandt, maar bedenk dat de spanning over beide lampjes in deze parallelschakeling gelijk zijn. Het lampje van 4 Ω heeft de grootste weerstand en dus de kleinste stroom. Het vermogen P = U · I van die lamp is dus het kleinst.

C Je denkt waarschijnlijk dat doordat de lampjes allebei dezelfde spanning krijgen zij even fel branden, maar beide lampjes zijn niet gelijk en branden dus niet even fel

D Je kunt de lampjes goed met elkaar vergelijken omdat de spanning bij beide lampjes gelijk is

Misvatting:

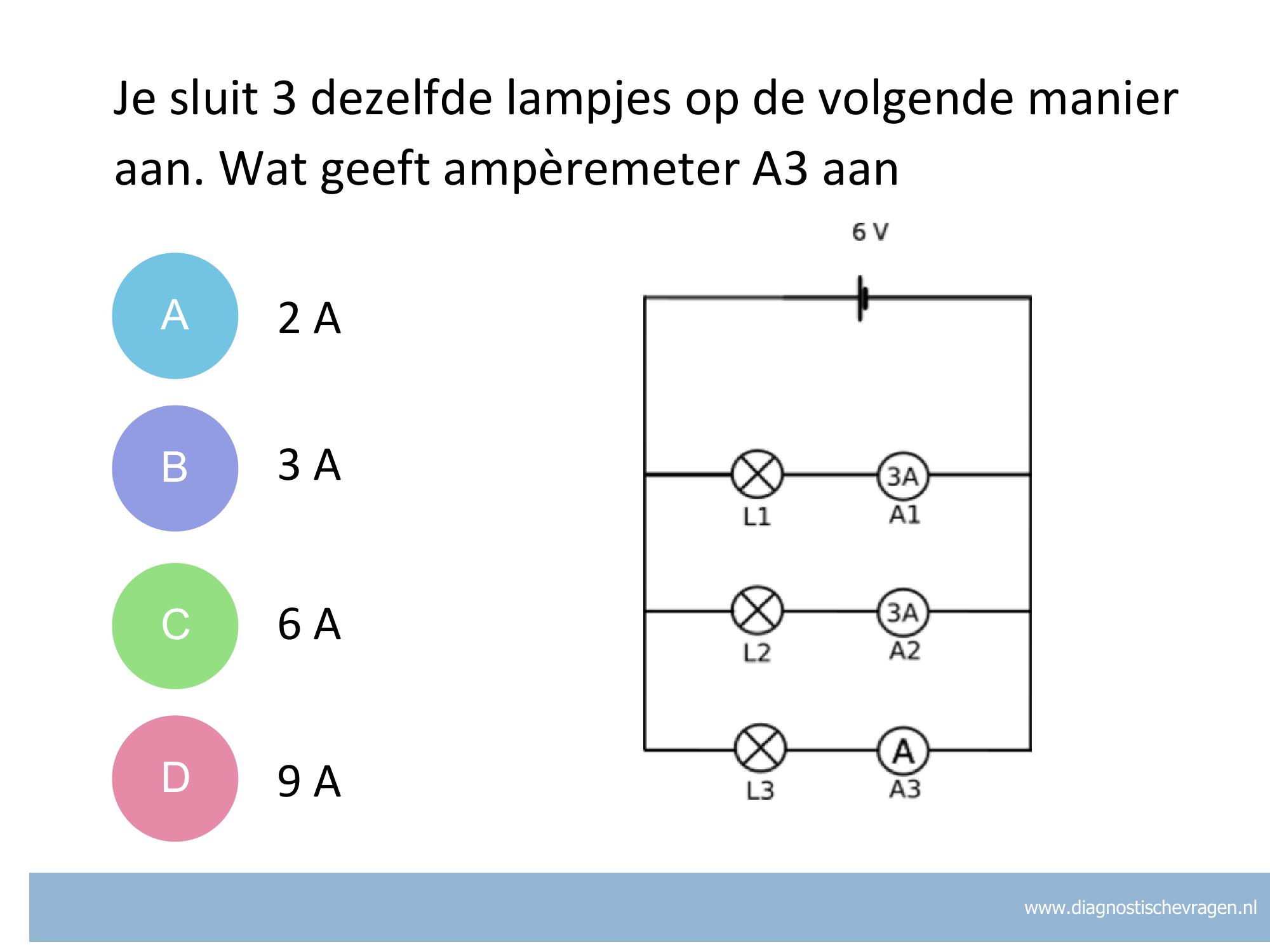
A Je denkt waarschijnlijk dat door het derde lampje is de totale weerstand toeneemt en 1,5 keer zo groot wordt, maar dat is niet zo. De stroomsterkte wordt niet 1,5 keer kleiner; dus geen 4 A. Door elk lampje gaat 3 A ( 6/2 ). Door het derde lampje gaat ook 3 A. De ampèremeter geeft nu 9 A aan.

B Je denkt waarschijnlijk dat de totale stroom (6 A) nu wordt verdeeld over drie lampjes in plaats van twee. In een parallelschakeling worden de echter deelstromen opgeteld. Schakel je dus een derde lampje erbij dan komt er een extra stroom bij. Door elk lampje gaat 3 A ( 6/2 ). Door het derde lampje gaat ook 3 A. De ampèremeter geeft nu 9 A aan.

C Correct. Door elk lampje gaat 3 A ( 6/2 ). Door het derde lampje gaat ook 3 A. De ampèremeter geeft nu 9 A aan.

Misvatting:

A Je denkt misschien dat de totale stroomsterkte (6 A) nu verdeeld moet worden over drie lampjes. Dan kom je op 2 A uit. Maar in een parallelschakeling staat juist de spanning vast. De spanning die de spanningsbron levert staat vast. Daarmee staat ook de spanning over het lampje vast. Dus kom je uit op 3 A.

B In een parallelschakeling is de spanning over elke component gelijk aan de spanning over de hele parallelschakeling. In dit geval dus 6 V. De lampjes zijn identiek, dus de stroomsterkte door lampje 3 is gelijk aan die door lampje 1 en door lampje 2. Dus 3 A.


C 6 A is de stroomsterkte door de eerste twee lampjes samen.

D Dit is de totale stroomsterkte die de batterij moet gaan leveren. Maar gevraagd is de stroomsterkte door lampje 3.

Misvatting:
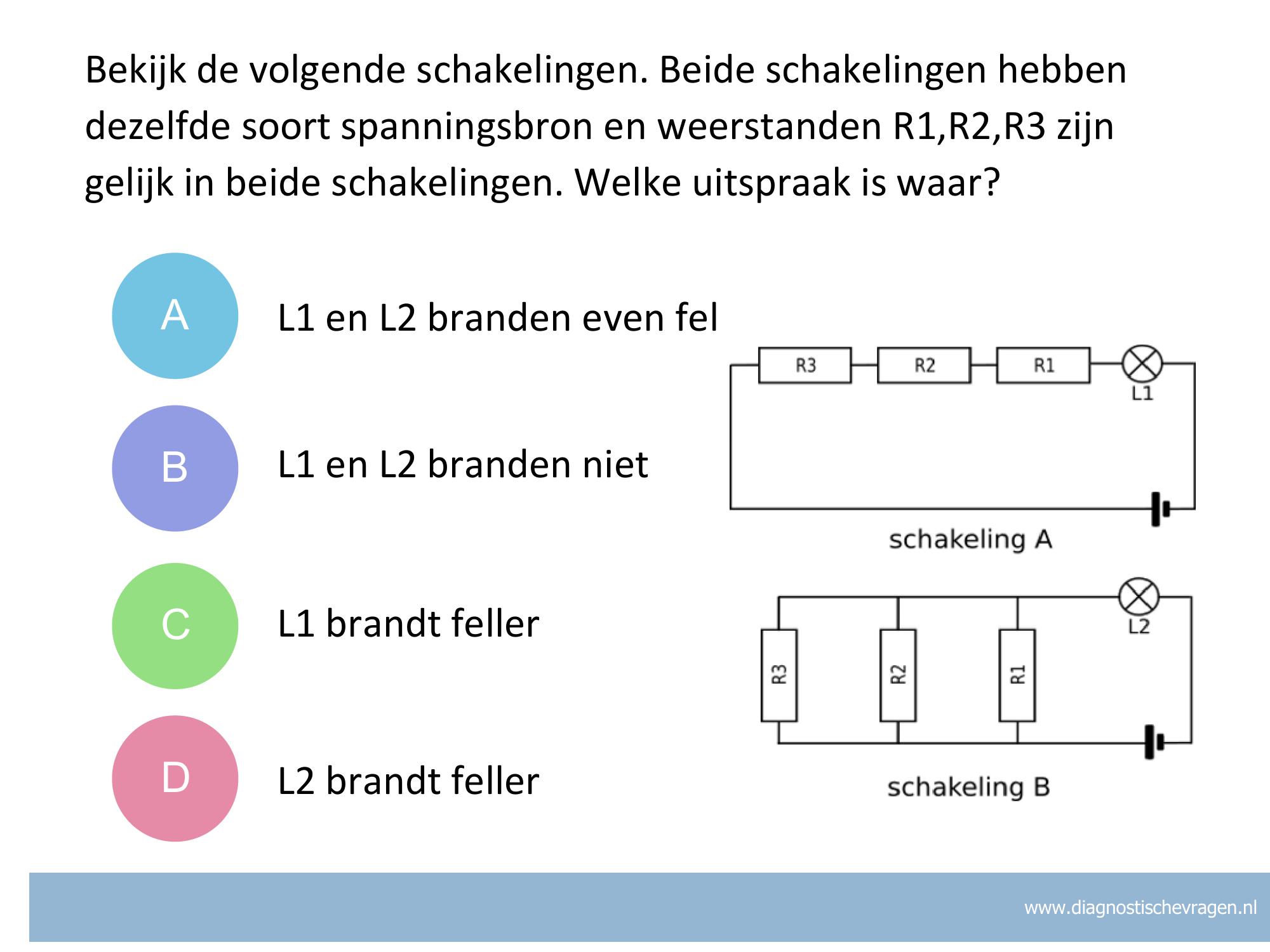
A Je denkt waarschijnlijk dat met dezelfde componenten de lampjes even fel branden, maar het maakt uit of de weerstanden in serie of parallel staan.

B Je denkt waarschijnlijk dat de weerstand te groot is, maar er loopt stroom door de lampjes, dus ze branden wel.

C De vervangingsweerstand van een parallelschakeling is kleiner dan die van een serieschakeling met dezelfde componenten. Meer weerstand betekend minder stroomsterkte, en dus een minder fel brandende lamp.

D Correct. In schakeling A staat het lampje in serie met drie weerstanden die onderling in serie staan. In schakeling B staat het lampje in serie met drie weerstanden die onderling parallel staan. De vervangingsweerstand van drie parallelle weerstanden is lager dan die van drie weerstanden in serie. De totale weerstand in schakeling B is dus lager. Bij dezelfde spanning is de stroomsterkte in schakeling B groter. Daardoor brandt het lampje feller.

Misvatting:

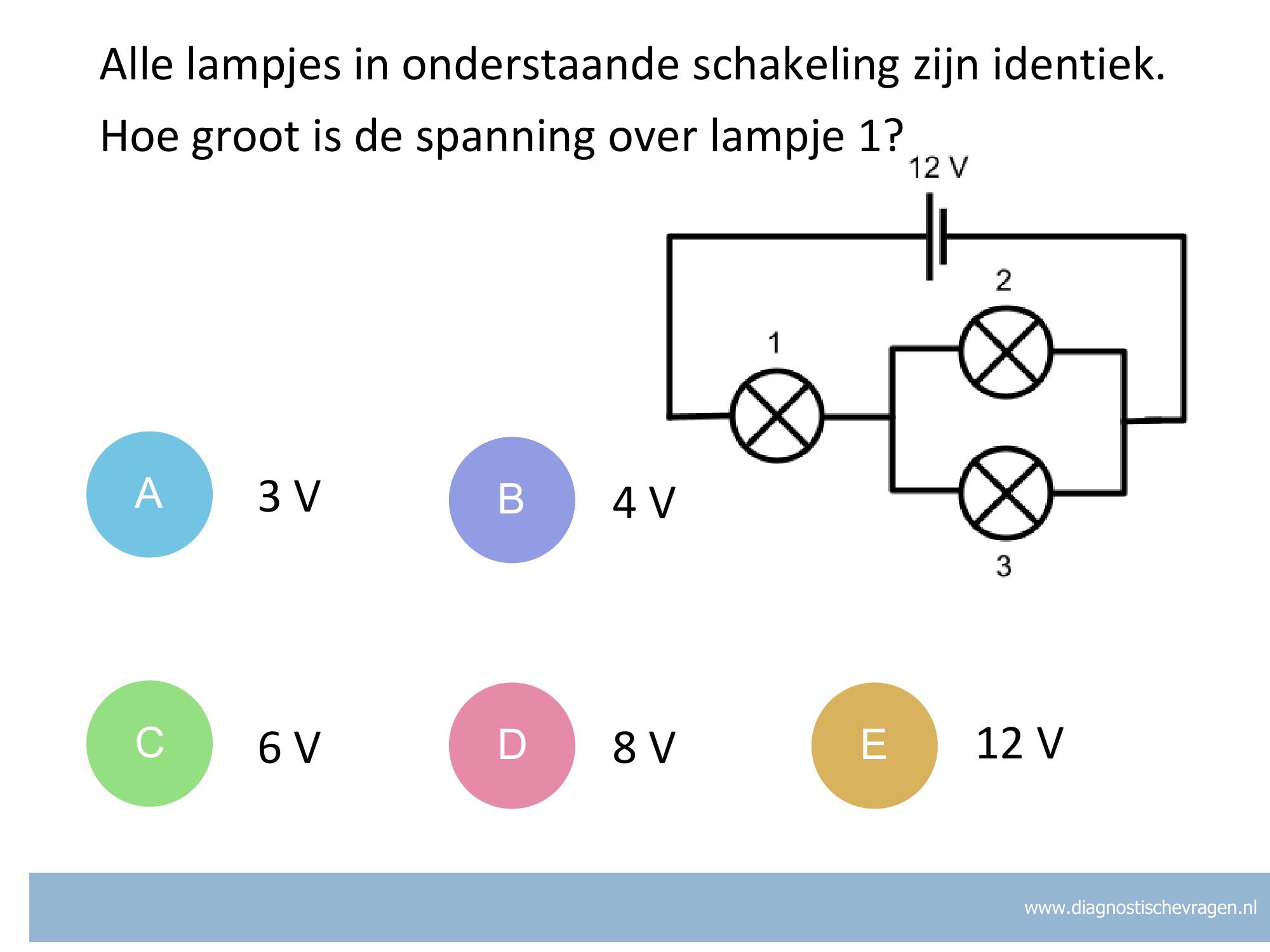
A In een serieschakeling verdeelt de spanning zich: grotere weerstand is grotere spanning. In deze opgave is de weerstand van lampje 1 groter dan de gecombineerde weerstand van lampje 2 en 3. Dus krijgt lampje 1 een grotere spanning dan lampje 2 en 3.

B Je denkt misschien dat de totale spanning verdeeld moet worden over drie lampjes, dus (12)/(3) = 4 V. maar dit geldt alleen als het een serieschakeling is, en dit is een combinatieschakeling.

C Je hebt misschien gezien dat de totale spanning van 12 V moet worden verdeeld over de twee componenten. Maar dat hoeft niet ‘eerlijk’ te worden verdeeld. Dat is alleen zo als allebei de componenten gelijk zijn. In dit geval is dat niet zo (want de ene is één lampje, de ander zijn twee lampjes parallel).

D Correct. De weerstand van lampje 2 en lampje 3 samen is de helft van die een los lampje 1/Rtot=1/R + 1/R Daarom is de spanning over lampje 2 en 3 de helft van de spanning over lampje 1. Die spanningen verhouden zich dus als 1:2. Omdat de totale spanning 12 V is, kom je uit op 4 V voor lampje 2 en dus 8 V voor lampje 1.



E Dit zou betekenen dat alle spanning over lampje 1 staat. Er is dan geen spanning met over voor lampje 2 en 3. Dat zou betekenen dat er ook geen stroom loopt in de schakeling.

Misvatting: Veel leerlingen denken dat een transformator de spanning niet omhoog kan brengen. Het lijkt dan namelijk dat er meer energie ontstaat. Maar als de spanning stijgt, dan daalt de stroomsterkte, waardoor het vermogen (energie per seconde) gelijk blijft (bij een ideale transformator) of afneemt (bij een realistische transformator)

A Correct. Een transformator kan de spanning omhoog transformeren

B Je denkt waarschijnlijk dat het vermogen omhoog wordt getransformeerd, maar het vermogen is afhankelijk van de spanning en de stroomsterkte en die verandert niet

C Je denkt waarschijnlijk dat het vermogen samen met de spanning omhoog wordt getransformeerd, maar als de spanning omhoog gaat, gaat de stroomsterkte naar beneden

D Je denkt waarschijnlijk dat een transformator de stroomsterkte omhoog kan transformeren

De vragen en toelichtingen vallen onder een CC BY-SA 4.0 licentie https://creativecommons.org/licenses/by-sa/4.0